Explore the fundamentals of the diode current equation with this in-depth guide. Learn how this pivotal formula dictates diode behavior in circuits through examples and numerical problems, enhancing your electronics knowledge.
The diode emerges as a pivotal component in the vast expanse of electronic circuit design and semiconductor physics. The diode current equation is central to understanding its operation, a mathematical representation that describes how current flows through a diode when subjected to a voltage. This article delves deep into the diode current equation, explicating its components, significance, and practical applications. We will also tackle some numerical problems to solidify your understanding and application of this fundamental equation.
Understanding the Diode Current Equation
The diode current equation, often called the Shockley ideal diode equation after William Shockley, encapsulates the relationship between the current flowing through a diode and its voltage. It is expressed as:
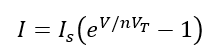
where:
- I is the diode current,
- IS is the saturation current (the current that flows through the diode when reverse-biased),
- V is the voltage across the diode,
- n is the ideality factor, typically ranging from 1 to 2, which accounts for the deviation from the ideal behavior due to recombination,
- VT is the thermal voltage, approximately 26mV at room temperature,
- e is the base of the natural logarithm, approximately equal to 2.71828.
This equation reveals how the diode’s current exponentially increases with a forward voltage, highlighting the non-linear characteristic of diodes that is crucial in electronics for tasks such as rectification, signal modulation, and voltage regulation.

Significance of Diode Equation in Circuit Design
The diode current equation is indispensable in circuit design and analysis. It allows engineers to predict the behavior of diodes in various conditions, facilitating the design of circuits that operate efficiently and reliably. Understanding this equation is essential for designing circuits that require precise control of current flow, such as in power supplies, signal processors, and electronic switching devices.
Numerical Problems on Diode Current Equation
Let’s dive into some numerical problems to apply the diode current equation and enhance our understanding. These problems are designed to enhance your proficiency with the diode current equation across various scenarios, including changes in ideality factor, temperature, and the determination of intrinsic diode parameters. As you work through these problems, you’ll gain a deeper understanding of the diode’s behavior in circuits, a critical skill for any electronics enthusiast or professional.
Problem 1: Calculating Forward Current
Given: A silicon diode at room temperature (25°C) with a saturation current (IS) of 10nA is subjected to a forward voltage (V) of 0.7V. Calculate the forward current (I) assuming an ideality factor (n) of 1.
Solution: First, calculate the thermal voltage (VT) at 25°C (298K):

Then, apply the diode current equation:
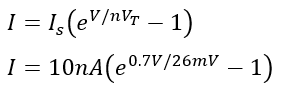
Problem 2: Determining Voltage Across the Diode
Given: A diode with a saturation current (IS) of 1nA has a current (I) of 5mA flowing through it at room temperature. Find the voltage (V) across the diode, using an ideality factor (n) of 1.
Solution: Start with the diode current equation and solve for V:
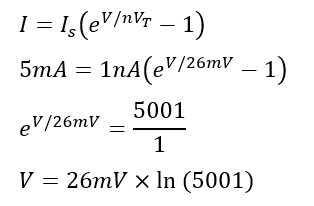
These problems illustrate the practical application of the diode current equation in real-world scenarios, enhancing your problem-solving skills and understanding of diode operations.
Problem 3: Reverse Saturation Current
Given: A germanium diode at room temperature (25°C) has a forward current of 2 mA when the forward voltage across it is 0.3V. Assuming the ideality factor (n) is 1, calculate the reverse saturation current (IS) of the diode.
Solution:
- First, recall the diode current equation:
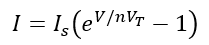
- Rearrange the equation to solve for Is
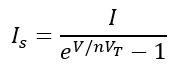
- Plug in the values (I=2mA, V=0.3V, n=1, and VT≈26mV) to find IS:
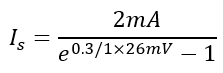
Problem 4: Ideality Factor Impact
Given: A diode with a reverse saturation current of 20 nA sees a forward voltage of 0.5V. Calculate the forward current through the diode for ideality factors of 1 and 2 at room temperature.
Solution:
Use the diode current equation:
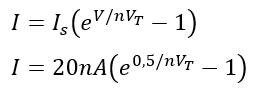
Calculate the forward current for n=1 and n=2, remembering VT≈26mV:
for n=1
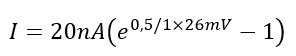
for n=2
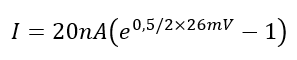
Problem 5: Temperature Effect on Forward Current
Given: A silicon diode with a reverse saturation current (IS) of 5 nA at 25°C is subjected to a forward bias of 0.7V. If the temperature increases to 35°C, calculate the new forward current (I). Assume the ideality factor (n) is 1. Remember, the thermal voltage (VT) varies with temperature, and VT=kT/q.

Conclusion
The diode current equation stands as a cornerstone in the study of electronics, offering profound insights into the behavior of diodes under various conditions. Its understanding is crucial for anyone venturing into electronics design, semiconductor physics, or electrical engineering. Through the exploration of this equation and the solving of numerical problems, we bridge the gap between theoretical concepts and their practical applications, ensuring a robust foundation in electronics and circuit design.