Depletion Width- Definition, Formula, Solved Problems

In semiconductor physics, the concept of depletion width is central to understanding the behavior of p-n junctions, which are fundamental components of various electronic devices such as diodes, transistors, and solar cells. The depletion region width describes the region around the p-n junction where mobile charge carriers (free electrons and holes) have been swept away, leaving behind a zone of fixed charged ions. This article delves into the definition of depletion width, provides its formula, derives this formula, and presents a solved example to illustrate the concept.

Definition of Depletion Width

In semiconductor physics, particularly in the study of p-n junctions, the depletion width refers to the region where mobile charge carriers (free electrons and holes) have been swept away due to the diffusion across the junction. This leaves behind a zone with only fixed charged ions, creating an electric field. The PN junction width is crucial in defining the electrical behavior of diodes, transistors, and other semiconductor devices.

Depletion Width Formula

The depletion width (𝑊) in a p-n junction can be expressed by the formula:

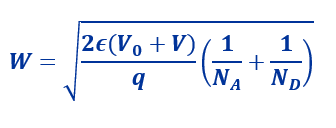
Where:

• ϵ is the permittivity of the semiconductor material,
• 𝑉_0​ is the built-in potential of the junction,
• 𝑉 is the externally applied voltage (positive for forward bias and negative for reverse bias),
• 𝑞 is the elementary charge (approximately1.6×10⁻¹⁹ Coulombs),
• 𝑁_𝐴 and 𝑁_𝐷​ are the acceptor and donor doping concentrations, respectively.

Depletion Width Formula Derivation

The derivation of the depletion width formula in a semiconductor junction (like a PN junction) involves understanding the behavior of charge carriers and electric fields at the interface between P-type and N-type semiconductors. The depletion region is where mobile charge carriers (electrons and holes) are absent, creating an area dominated by the immobile ionized donor and acceptor impurities. Here’s a step-by-step derivation:

Step 1: Basic Assumptions

1. Uniform Doping: Assume the P-type and N-type regions are uniformly doped with acceptor density 𝑁𝐴​ and donor density 𝑁𝐷​, respectively.
2. One-dimensional Analysis: Consider only the one-dimensional case along the x-axis across the PN junction.

Step 2: Charge Neutrality

The total charge in the depletion region must be zero for overall electrical neutrality: 𝑄𝑝+𝑄𝑛=0 where:

• 𝑄_𝑝=−𝑞𝑁_𝐴𝑊_𝑝​​ is the charge in the P-type depletion region.
• 𝑄_𝑛=𝑞𝑁_𝐷𝑊_𝑛​ is the charge in the N-type depletion region.
• 𝑊_𝑝​ and 𝑊_𝑛​ are the widths of the depletion regions in the P-type and N-type materials, respectively.
• 𝑞 is the elementary charge.

Step 3: Relationship Between Wp​ and Wn​

Using charge neutrality:
𝑁_𝐴𝑊_𝑝=𝑁_𝐷𝑊_𝑛

This can be rearranged to relate the widths of the depletion regions:

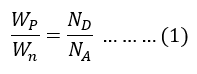
Step 4: Electric Field and Potential Drop

The electric field 𝐸 reaches its maximum at the metallurgical junction with:

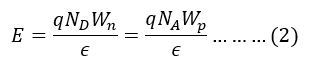
Where 𝜖 is the permittivity of the semiconductor.

By integrating the electric field across the depletion region, the built-in voltage V₀​ (also called the contact potential) is found:

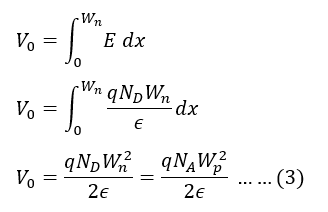
​​Step 5: Total Depletion Width 𝑊

The total width 𝑊

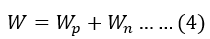
Using the charge neutrality and the relationship between 𝑊𝑝 and 𝑊𝑛​:

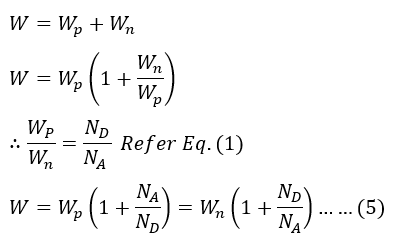
Step 6: Solving for 𝑊

Substitute the expression for 𝑊𝑛 or 𝑊𝑝​ from the potential drop:

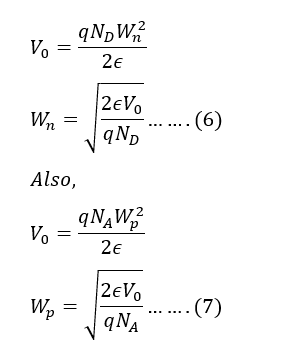
Then, the total depletion width W is given by:

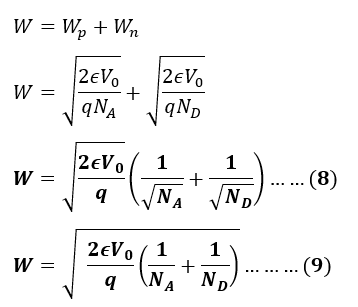
If external voltage (V) is applied to the PN junction and the diode is in reverse bias, the depletion region is,

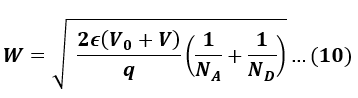
If external voltage (V) is applied to the PN junction and the diode is in forward bias, the depletion region is,

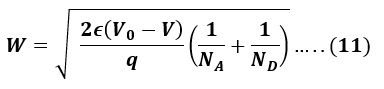
This formula quantifies the width of the depletion region as a function of the doping concentrations, the permittivity of the material, and the built-in voltage across the junction. It’s fundamental in understanding how PN junctions behave under different electrical and environmental conditions.

Solved Problem

A silicon PN junction at room temperature and its width are used as an example to solidify understanding of the theoretical derivation.

Problem-1

A silicon PN junction at room temperature (300 K) has a uniform acceptor concentration 𝑁_𝐴=10¹⁶ cm⁻³ in the P-type region and a donor concentration 𝑁_𝐷=5×10¹⁶ cm⁻³ in the N-type region. Assume the built-in potential 𝑉₀​ is 0.7 V. Calculate the depletion width of this junction.

Constants

• Elementary charge, 𝑞=1.6×10⁻¹⁹ C
• Relative permittivity of silicon, 𝜖_𝑟=11.7
• Permittivity of free space, 𝜖₀=8.854×10⁻¹⁴ F/cm
• Permittivity of silicon, 𝜖=𝜖_𝑟𝜖₀

Solution

Step 1: Calculate the permittivity of silicon

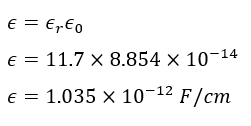
Step 2: Apply the PN Junction width formula

Using the formula:

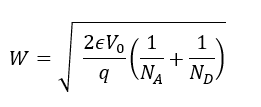
We substitute the given values:

Problem-2

Consider a silicon PN junction with an acceptor concentration 𝑁_𝐴=10¹⁷ cm⁻³ in the P-type region and a donor concentration 𝑁_𝐷=10¹⁶ cm⁻³ in the N-type region. The built-in potential 𝑉₀ is 0.8 V. Calculate the depletion width when a reverse bias of 5 V is applied to the junction.

Constants

• Elementary charge, 𝑞=1.6×10⁻¹⁹ C
• Relative permittivity of silicon, 𝜖_𝑟=11.7
• The permittivity of free space, 𝜖₀=8.854×10⁻¹⁴ F/cm

Solution

Step 1: Calculate the permittivity of silicon

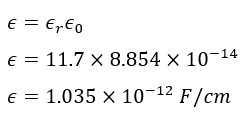
Step 2: Calculate W

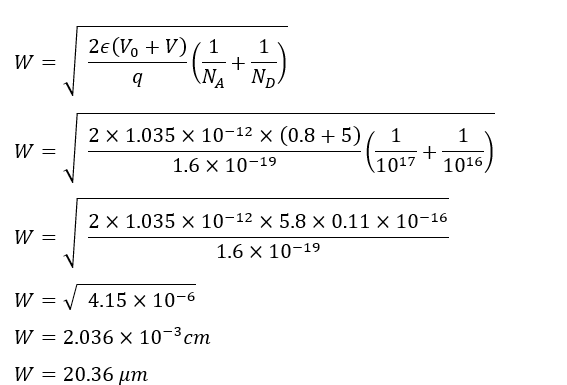
Conclusion

In conclusion, the study of depletion width in PN junctions provides a fundamental insight into the operational principles of semiconductor devices, from defining what depletion width is and why it forms to deriving its quantitative formula and applying this knowledge through solved examples.

1. Diode Current Equation
2. Diffusion Capacitance
3. What is a Diode?
4. Ringing in Power Diode
5. Knee Voltage in Diode