What is Reverse Saturation Current?

Definition: Reverse saturation current, often denoted by 𝐼_𝑆​ or 𝐼₀​, is a small current that flows through a diode even when it is reverse-biased. This current is generally due to the drift of charge carriers (electrons and holes) across the junction without an external forward voltage.

Reasons for Reverse Saturation Current:

1. Thermal Generation of Electron-Hole Pairs: In semiconductors, thermal energy can cause the breaking of covalent bonds, generating electron-hole pairs. Due to the ambient temperature, these carriers are present without an external voltage.
2. Minority Carrier Injection: In the reverse bias condition, the minority carriers in the p-type and n-type regions gain enough energy from the thermal environment to cross the depletion region, contributing to the reverse current.

Formula for Reverse Saturation Current:

The reverse saturation current in a pn-junction diode can be expressed by the formula:

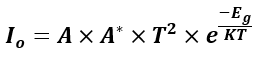
Where:

• 𝐴 is the diode area
• 𝐴^∗ (often called Richardson’s constant) depends on the material properties
• 𝑇 is the absolute temperature (in Kelvin)
• 𝐸_𝑔​ is the bandgap energy of the semiconductor
• 𝑘 is the Boltzmann constant
• 𝑒 is the base of the natural logarithm

This formula shows that 𝐼₀​ increases with temperature and depends inversely on the bandgap energy of the semiconductor.

Solved Example:

Calculate the reverse saturation current for a silicon diode at 300K given that the diode’s area is 1×10⁻⁶ m², Richardson’s constant for silicon is 120A/cm²⋅K², and the bandgap energy is 1.1 eV. Also Calculate the reverse saturation current at 350K.

Solution:

1 eV=1.6×10⁻¹⁹ Joules
Eg= 1.1×1.6×10⁻¹⁹ Joules
Diode Area(A)= 1×10⁻⁶ m²
A= 1×10⁻⁶ ×100 ×100 cm²
A= 10^-2 cm²

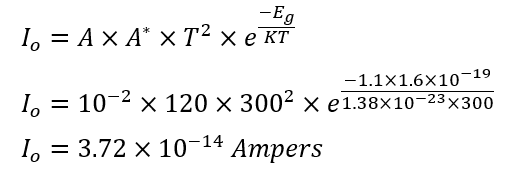
Reverse current at 350K,

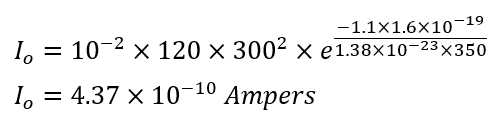
This calculation illustrates how significantly the reverse saturation current can increase with just a 50 K increase in temperature, highlighting the exponential sensitivity of semiconductor devices to temperature changes

Diode current under Reversed Bias

The diode current (𝐼I) under any bias condition can be expressed by the Shockley diode equation:

Where:

• 𝐼 is the diode current.
• 𝐼₀​ is the reverse saturation current.
• 𝑉 is the voltage across the diode.
• q is the charge of an electron (1.6×10⁻¹⁹ Coulombs).
• k is Boltzmann’s constant (1.38×10⁻²³ J/K).
• T is the absolute temperature in Kelvin.
• n is the ideality factor, typically ranging from 1 to 2, which accounts for the deviation of the diode from ideal behavior.

In the reverse bias condition (𝑉<0), therefore V has a negative value,

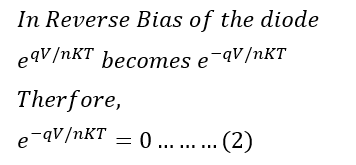
Putting the value of equation (2) in equation(1),

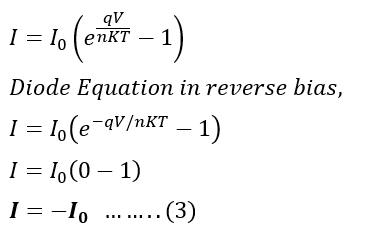
Thus, I≈−I₀​ means the diode current approximately equals the reverse saturation current but with the opposite sign. This shows 𝐼_0​ directly defines the magnitude of the leakage current in reverse bias.

1. Forward Bias and Reverse Bias of PN Junction
2. Diode Ideality Factor
3. Ideal diode
4. Depletion Width of PN Junction Diode
5. Diffusion Capacitance of Diode